The clFFT library is an OpenCL library implementation of discrete Fast Fourier Transforms. The library:
The FFT is an implementation of the Discrete Fourier Transform (DFT) that makes use of symmetries in the FFT definition to reduce the mathematical intensity required from O( \(N^2\)) to O( \( N \log N\)) when the sequence length, N, is the product of small prime factors. Currently, there is no standard API for FFT routines. Hardware vendors usually provide a set of high-performance FFTs optimized for their systems: no two vendors employ the same interfaces for their FFT routines. clFFT provides a set of FFT routines that are optimized for AMD graphics processors, and that are also functional across CPU and other compute devices.
clFFT supports transform sizes that are powers of 2, 3, 5, and 7. This means that the vector lengths can be a combination of powers of two, three, five, and seven; examples include \(2^7, 2^1*3^1, 3^2*5^4, 2^2*3^3*5^5\), up to the limit that the device can support.
Currently, there is an upper bound on the transform size that the library can support for certain transforms. This limit is \(2^{24}\) for real 1D single precision and \(2^{22}\) for real 1D double precision.
clFFT currently supports FFTs of (up to) three dimensions, given by the enum clfftDim. This enum is a required parameter of clfftCreateDefaultPlan() to create an initial plan, where a plan is the collection of (almost) all the parameters needed to specify an FFT computation. For more information about clFFT plans, see the section clFFT plans. Depending on the dimensionality that the client requests, clFFT uses the following formulations to compute the DFT:
\[ {\tilde{x}}_j = {{1}\over{scale}}\sum_{k=0}^{n-1}x_k\exp\left({\pm i}{{2\pi jk}\over{n}}\right)\hbox{ for } j=0,1,\ldots,n-1 \]
where, \(x_k\) are the complex data to be transformed, \(\tilde{x}_j\) are the transformed data, and the sign \(\pm\) determines the direction of the transform: \(-\) for forward and \(+\) for backward. Note that you must provide the scaling factor. By default, the scale is set to 1 for forward transforms, and \({{1}\over{N}}\) for backward transforms, where N is the size of transform.\[ {\tilde{x}}_{jk} = {{1}\over{scale}}\sum_{q=0}^{m-1}\sum_{r=0}^{n-1}x_{rq}\exp\left({\pm i} {{2\pi jr}\over{n}}\right)\exp\left({\pm i}{{2\pi kq}\over{m}}\right) \]
for \(j=0,1,\ldots,n-1\hbox{ and } k=0,1,\ldots,m-1\), where, \(x_{rq}\) are the complex data to be transformed, \(\tilde{x}_{jk}\) are the transformed data, and the sign \(\pm\) determines the direction of the transform. By default, the scale is set to 1 for forwards transforms and \({{1}\over{MN}}\) for backwards transforms, where M and N are the 2D size of the transform.\[ \tilde{x}_{jkl} = {{1}\over{scale}}\sum_{s=0}^{p-1}\sum_{q=0}^{m-1}\sum_{r=0}^{n-1} x_{rqs}\exp\left({\pm i} {{2\pi jr}\over{n}}\right)\exp\left({\pm i}{{2\pi kq}\over{m}}\right)\exp\left({\pm i}{{2\pi ls}\over{p}}\right) \]
for \(j=0,1,\ldots,n-1\hbox{ and } k=0,1,\ldots,m-1\hbox{ and } l=0,1,\ldots,p-1\), where \(x_{rqs}\) are the complex data to be transformed, \(\tilde{x}_{jkl}\) are the transformed data, and the sign \(\pm\) determines the direction of the transform. By default, the scale is set to 1 for forward transforms and \({{1}\over{MNP}}\) for backward transforms, where M, N, and P are the 3D size of the transform.clFFT is initialized by the API clfftSetup(), which must be called before any other API of clFFT. This allows the library to create resources needed to manage the plans that you create and destroy. This API also takes a structure clfftInitSetupData() that is initialized by the client to control the behavior of the library.
After you use the library, the clfftTeardown() method must be called. This function instructs clFFT to release all resources allocated internally, and resets acquired references to any OpenCL objects.
The clFFT API is designed to be thread-safe. It is safe to create plans from multiple threads and to destroy those plans in separate threads. Multiple threads can call clfftEnqueueTransform() to place work in a command queue at the same time. clFFT does not provide a single-threaded version of the library. The overhead of the synchronization mechanisms inside a clFFT thread-safe is expected to be minor.
Currently, you must manage the multi-device operation. You can create OpenCL contexts that are associated with multiple devices, but clFFT only uses a single device from that context to transform the data. You can manage a multi-device operation by creating multiple contexts, in which each context contains a different device; you are responsible for scheduling and partitioning the work across multiple devices and contexts.
clFFT expects all multi-dimensional input passed to it to be in row-major format. This is compatible with C-based languages. However, clFFT is very flexible in the organization of the input and output data, and it accepts input data by letting you specify a stride for each dimension. This feature can be used to process data in column major arrays and other non-contiguous data formats. See clfftSetPlanInStride() and clfftSetPlanOutStride().
Your application must allocate and manage OpenCL objects, such as contexts, cl_mem buffers and command queues. All the clFFT interfaces that interact with OpenCL objects take those objects as references through the API. Specifically, the plan creation function clfftCreateDefaultPlan() takes an OpenCL context as a parameter reference, increments the reference count on that object, and keeps the object alive until the corresponding plan is destroyed by the call clfftDestroyPlan().
The clFFT API operates asynchronously; with the exception of thread safety locking with multiple threads, all APIs return immediately. Specifically, the clfftEnqueueTransform() API does not explicitly flush the command queues that are passed by reference to it. It pushes the transform work onto the command queues and returns the modified queues to the client. The client is free to issue its own blocking logic by using OpenCL synchronization mechanisms or push further work onto the queue to continue processing.
The clFFT library looks for definition of two environment variables: CLFFT_CACHE_PATH and CLFFT_REQUEST_LIB_NOMEMALLOC. If the variable CLFFT_CACHE_PATH is defined, the library caches OpenCL binaries. This enables a subsequent run of the application with the same type of transforms to avoid the expensive compilation step. Instead, the stored binaries are loaded and executed. The CLFFT_CACHE_PATH must point to a folder location where the library can store binaries. The other variable CLFFT_REQUEST_LIB_NOMEMALLOC when defined, requests the library to do all computations in-place and avoid allocating extra device memory whenever possible. This feature is experimental and currently works only for certain types of transforms when the library decomposes the input into square matrices or rectangular matrices with dimensions in the ratio 1:2. Currently, it works for 1D complex transforms of size of powers of 2.
A plan is the collection of (almost) all the parameters needed to specify an FFT computation. A clFFT plan includes the following parameters:
The clFFT plan does not include the following parameters:
These parameters are specified when the plan is executed.
When a new plan is created by calling clfftCreateDefaultPlan(), its parameters are initialized as follows:
Writing client programs that depend on these initial values is not recommended.
There are two main types of Discrete Fourier Transform (DFT) in clFFT:
For one-dimensional data, if clStrides[0] = strideX = 1, successive elements in the first dimension are stored contiguously in memory. If strideX is an integral value greater than 1, gaps in memory exist between each element of the vectors. For multi-dimensional data, if clStrides[1] = strideY = LenX for 2 dimensional data and clStrides[2] = strideZ = LenX*LenY for 3 dimensional data, no gaps exist in memory between each element, and all vectors are stored tightly packed in memory. Here, LenX, LenY, and LenZ denote the transform lengths clLengths[0], clLengths[1], and clLengths[2], respectively, which are used to set up the plan.
By specifying non-default strides, it is possible to process either row-major or column-major arrays. Data can be extracted from arrays of structures. Almost any regular data storage pattern can be accommodated.
Distance is the amount of memory that exists between corresponding elements in an FFT primitive in a batch. Distance is measured in units of the FFT primitive; complex data measures in complex units, and real data measures in real units. Stride between tightly packed elements is 1 in either case. Typically, one can measure the distance between any two elements in a batch primitive, be it 1D, 2D, or 3D data. For tightly packed data, the distance between FFT primitives is the size of the FFT primitive, such that dist=LenX for 1D data, dist=LenX*LenY for 2D data, and dist=LenX*LenY*LenZ for 3D data. It is possible to set the distance of a plan to be less than the size of the FFT vector; most often 1 for this case. When computing a batch of 1D FFT vectors, if distance == 1, and strideX == length(vector), a transposed output is produced for a batch of 1D vectors. You must verify that the distance and strides are valid (not intersecting); if not valid, undefined results may occur. A simple example would be to perform a 1D length 4096 on each row of an array of 1024 rows x 4096 columns of values stored in a column-major array, such as a FORTRAN program might provide. (This would be equivalent to a C or C++ program that has an array of 4096 rows x 1024 columns stored in a row-major manner, on which you want to perform a 1-D length 4096 transform on each column.) In this case, specify the strides as [1024, 1].
A more complex example would be to compute a 2D FFT for each 64 x 64 subtile of the grid that has an input buffer with a raster grid of 1024 x 1024 monochrome pixel values. Specifying strides allows you to treat each horizontal band of 1024 x 64 pixels as an array of 16 64 x 64 matrixes, and process an entire band with a single call clfftEnqueueTransform(). (Specifying strides is not quite flexible enough to transform the entire grid of this example with a single kernel execution.) It is possible to create a Plan to compute arrays of 64 x 64 2D FFTs, then specify three strides: [1, 1024, 64]. The first stride, 1, indicates that the rows of each matrix are stored consecutively; the second stride, 1024, gives the distance between rows, and the third stride, 64, defines the distance between two matrices. Then call clfftEnqueueTransform() 16 times – once for each horizontal band of pixels.
Both CLFFT_SINGLE and CLFFT_DOUBLE precisions are supported by the library for all supported radices. For both these enums the math functions of the host computer are used to produce the sine and cosine tables that are used by the OpenCL kernel. Both CLFFT_SINGLE_FAST and CLFFT_DOUBLE_FAST generate faster kernels with reduced accuracy, but are disabled in the current build. See clfftPrecision, clfftSetPlanPrecision(), and clfftGetPlanPrecision().
For complex transforms, the direction of the transform is not baked into the plan; the same plan can be used to specify both forward and backward transforms. To specify the direction, clfftDirection is passed as a parameter into clfftEnqueueTransform(). For real transforms, the input and output layouts of the plan determine the direction.
The clFFT API supports both in-place and out-of-place transforms. With in-place transforms, only the input buffers are provided to the clfftEnqueueTransform() API, and the resulting data is written in the same buffer, overwriting the input data. With out-of-place transforms, distinct output buffers are provided to the clfftEnqueueTransform() API, and the input data is preserved. In-place transforms require that the cl_mem objects created by the client application, have both read and write permissions. This is given in the nature of the in-place algorithm. Out-of-place transforms require that the destination buffers have read and write permissions, but input buffers can still be created with read-only permissions. This is a clFFT requirement because internally the algorithms may go back and forth between the destination buffers and internally allocated temp buffers. For out-of-place transforms, clFFT never writes back to input buffers.
The efficiency of clFFT is improved by utilizing transforms in batches. Sending as much data as possible in a single transform call leverages the parallel compute capabilities of OpenCL devices (and GPU devices in particular), and minimizes the penalty of transfer overhead. It is best to think of an OpenCL device as a high-throughput, high-latency device. Using a networking analogy as an example, this approach is similar to having a massively high-bandwidth pipe with very high ping response times. If the client is ready to send data to the device for compute, it should be sent in as few API calls as possible and this can be done by batching. clFFT plans have a parameter clfftSetPlanBatchSize() to describe the number of transforms being batched, and another parameter clfftSetPlanDistance() to describe how those batches are laid out and spaced in memory. 1D, 2D, or 3D transforms can be batched.
To perform FFT calculations using clFFT, the client program must perform the following tasks:
For each distinct type of FFT needed:
When real data is subject to DFT transformation, the resulting complex output data follows a special property. About half of the output is redundant because they are complex conjugates of the other half. This is called the Hermitian redundancy. So, for space and performance considerations, it is only necessary to store the non-redundant part of the data. Most FFT libraries use this property to offer specific storage layouts for FFTs involving real data. clFFT provides three enumerated types to deal with real data FFTs:
The CLFFT_REAL enum specifies that the data is purely real. This can be used to feed real input or get back real output. The CLFFT_HERMITIAN_INTERLEAVED and CLFFT_HERMITIAN_PLANAR enums are similar to the corresponding full complex enums in the way they store real and imaginary components, but store only about half of the complex output. Client applications can do just a forward transform and analyze the output or they can process the output and do a backward transform to get back real data. This is illustrated in the following figure.
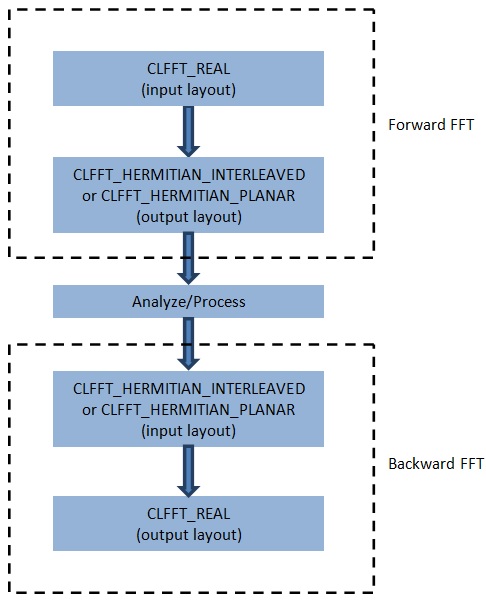
Let us consider a 1D real FFT of length N. The full output looks as shown in following figure.

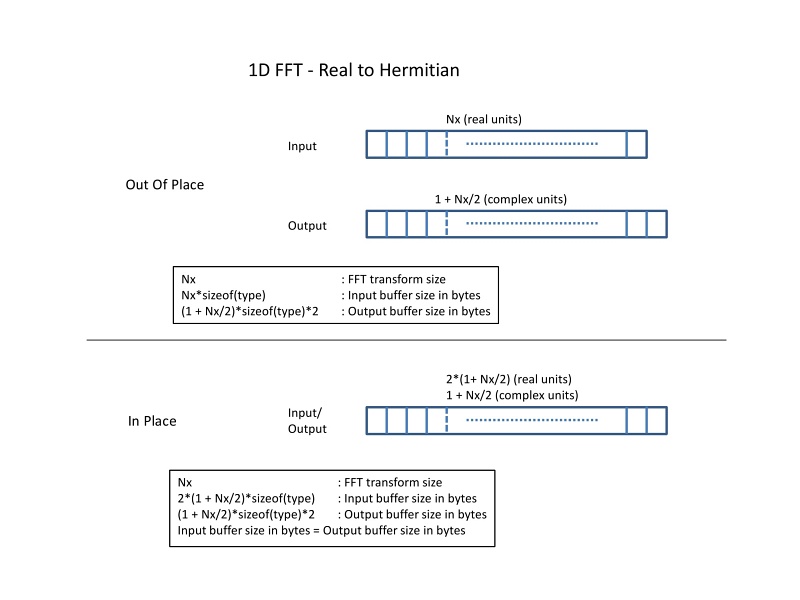
Here, C* denotes the complex conjugate. Since the values at indices greater than N/2 can be deduced from the first half of the array, clFFT stores data only up to the index N/2. This means that the output contains only 1 + N/2 complex elements, where the division N/2 is rounded down. Examples for even and odd lengths are given below.
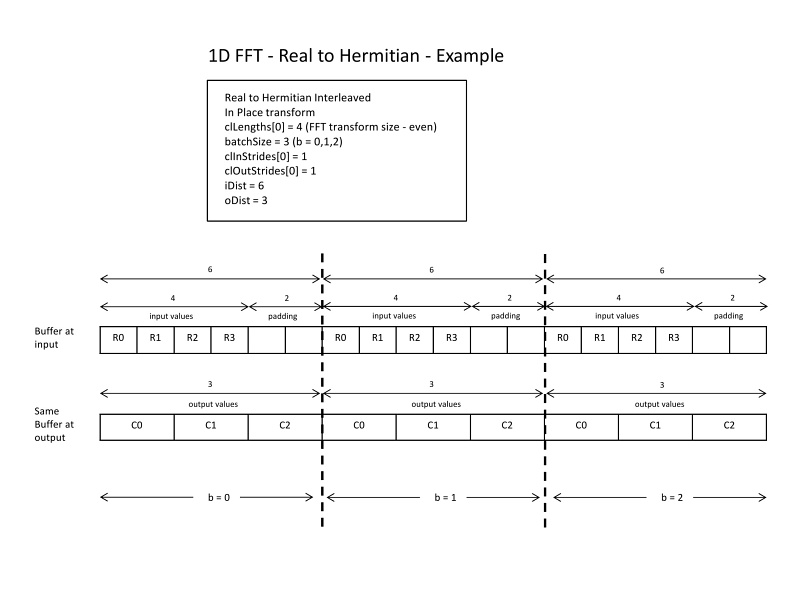
Example for N = 8 is shown in following figure.

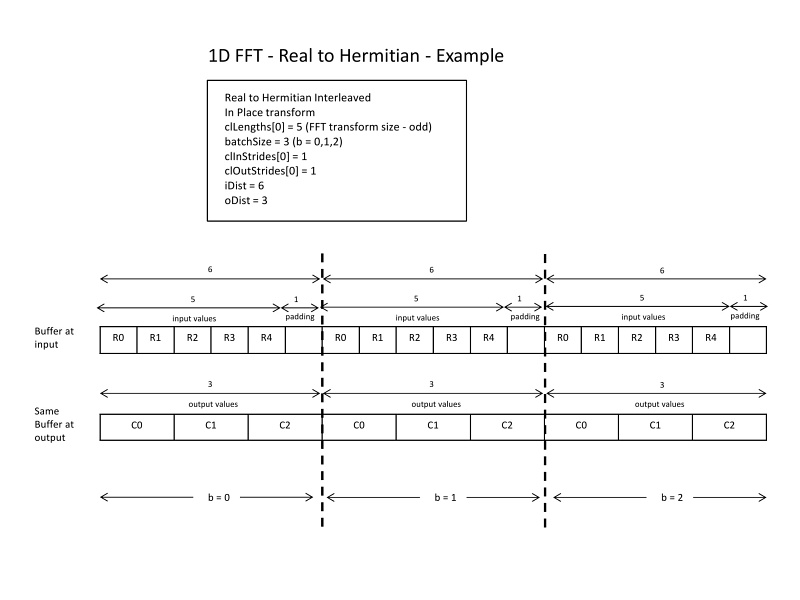
Example for N = 7 is shown in following figure.

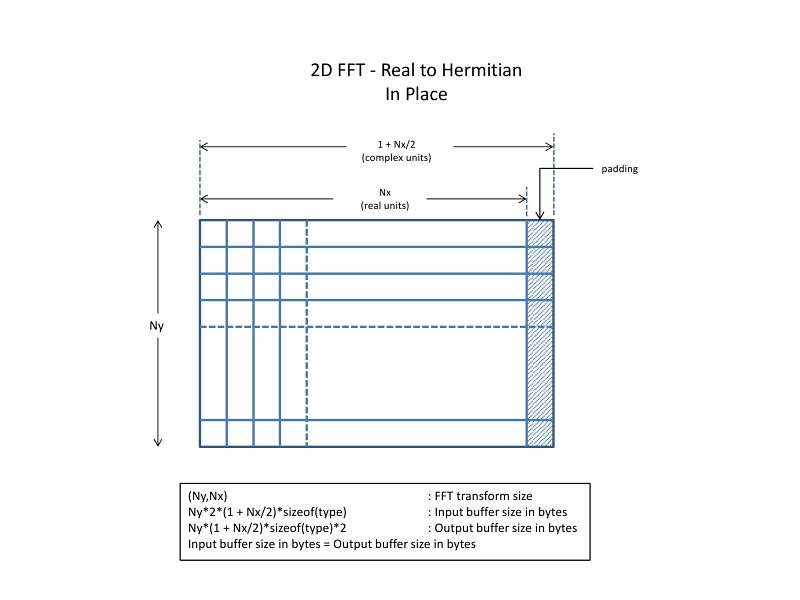
For length 8, only (1 + 8/2) = 5 of the output complex numbers are stored, with the index ranging from 0 through 4. Similarly for length 7, only (1 + 7/2) = 4 of the output complex numbers are stored, with the index ranging from 0 through 3. For 2D and 3D FFTs, the FFT length along the least dimension is used to compute the (1 + N/2) value. This is because the FFT along the least dimension is computed first and is logically a real-to-hermitian transform. The FFTs along other dimensions are computed afterwards; they are simply 'complex-to-complex' transforms. For example, assuming clLengths[2] is used to set up a 2D real FFT, let N1 = clLengths[1], and N0 = clLengths[0]. The output FFT has N1*(1 + N0/2) complex elements. Similarly, for a 3D FFT with clLengths[3] and N2 = clLengths[2], N1 = clLengths[1], and N0 = clLengths[0], the output has N2*N1*(1 + N0/2) complex elements.
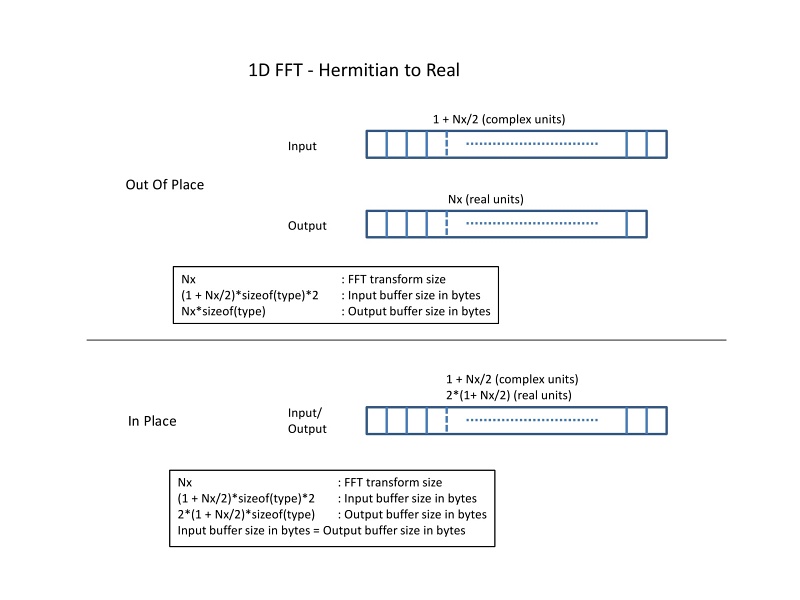
Out-of-place transforms:
In-place transforms:
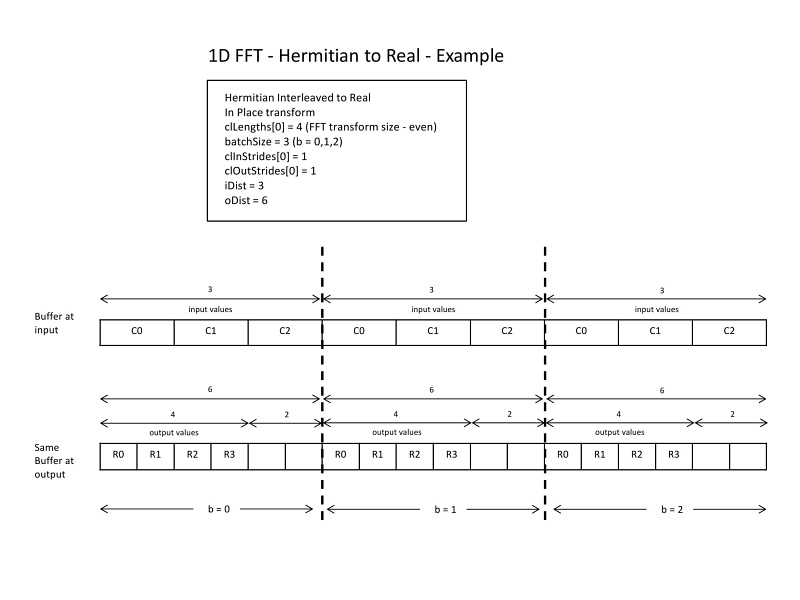
The library currently requires you to explicitly set input and output strides for real transforms. See the following examples to understand what values to use for input and output strides under different scenarios. These examples show typical usages, but you can allocate the buffers and layout data according to your need.
The following pages provide figures and examples to explain in detail the real FFT features of this library.


The callback feature of clFFT has the ability to invoke user provided OpenCL™ inline functions to pre-process or post-process data from within the FFT kernel. The inline OpenCL callback function is passed as a string to the library. It is then incorporated into the generated FFT kernel. This eliminates the need for an additional kernel launch to carry out the pre/post processing tasks, thus improving overall performance. There are 2 types of callback; Pre-callback and Post-callback. Pre-callback invokes user callback function to perform custom pre-processing of the input data before FFT is executed. Post-callback invokes user callback function to perform custom post-processing of the output data after FFT is executed.
The workflow of FFT execution using callback feature of clFFT is as follows:
The caller is responsible to provide a callback function that matches the function prototype based on the type of callback(pre/post), type of transform(real/complex) and whether LDS is used. The bake plan step checks the function prototype.
clFFT expects the callback function to be of a specific prototype depending on the type of callback(pre/post), type of transform(real/complex) and whether LDS is used. These are as follows:
| FFT Type | Function Prototype |
|---|---|
| C2C/C2R – Interleaved Single Precision | Without LDS float2 <precallback_func> ( __global void *input, uint inoffset, __global void *userdata) With LDS float2 <precallback_func> ( __global void *input, uint inoffset, __global void *userdata, __local void *localmem) |
| C2C/C2R – Interleaved Double Precision | Without LDS double2 <precallback_func> ( __global void *input, uint inoffset, __global void *userdata) With LDS double2 <precallback_func> ( __global void *input, uint inoffset, __global void *userdata, __local void *localmem) |
| C2C – Planar Single Precision | Without LDS float2 <precallback_func> ( __global void *inputRe, __global void *inputIm, uint inoffset, __global void *userdata) With LDS float2 <precallback_func> ( __global void *inputRe, __global void *inputIm, int inoffset, __global void *userdata, __local void *localmem) |
| C2C – Planar Double Precision | Without LDS double2 <precallback_func> ( __global void *inputRe, __global void *inputIm, uint inoffset, __global void *userdata) With LDS double2 <precallback_func> ( __global void *inputRe, __global void *inputIm, uint inoffset, __global void *userdata, __local void *localmem) |
| R2C Single Precision | Without LDS float <precallback_func> ( __global void *input, uint inoffset, __global void *userdata) With LDS float <precallback_func> ( __global void *input, uint inoffset, __global void *userdata, __local void *localmem) |
| R2C Double Precision | Without LDS double <precallback_func> ( __global void *input, uint inoffset, __global void *userdata) With LDS double <precallback_func> ( __global void *input, uint inoffset, __global void *userdata, __local void *localmem) |
Parameters
input : The base pointer of the input buffer for R2C and Interleaved C2C/C2R transforms inputRe : The base pointer of the “Real” input buffer for Planar C2C transforms inputIm : The base pointer of the “Imaginary” part input buffer for Planar C2C transforms inoffset : Index of the current element of the input buffer from the start userdata : Buffer containing optional caller specified data. The userdata pointer is useful for passing any supplementary data to the callback function. For example, buffer having convolution filter data or any scalar value. The userdata can be of any custom data type/structure, in which case, you have to declare the custom data type and include it along with the callback function string. localmem : Pointer to local memory. This memory is allocated by library based on the size you specify and is subjected to local memory availability. For Planar C2C, the return type of callback is a vector (float2/double2) that contains the Real and Imaginary elements as computed in the callback.
| FFT Type | Function Prototype |
|---|---|
| C2C/R2C – Interleaved Single Precision | Without LDS void <postcallback_func> ( __global void *output, uint outoffset, __global void *userdata, float2 fftoutput) With LDS void <postcallback_func> ( __global void *output, uint outoffset, __global void *userdata, float2 fftoutput, __local void *localmem) |
| C2C/R2C – Interleaved Double Precision | Without LDS void <postcallback_func> ( __global void *output, uint outoffset, __global void *userdata, double2 fftoutput) With LDS void <postcallback_func> ( __global void *output, uint outoffset, __global void *userdata, double2 fftoutput, __local void *localmem) |
| C2C/R2C – Planar Single Precision | Without LDS void <postcallback_func> ( __global void *outputRe, __global void *outputIm, uint outoffset, __global void *userdata, float fftoutputRe, float fftoutputIm) With LDS void <postcallback_func> ( __global void *outputRe, __global void *outputIm, uint outoffset, __global void *userdata, float fftoutputRe, float fftoutputIm, __local void *localmem) |
| C2C/R2C – Planar Double Precision | Without LDS void <postcallback_func> ( __global void *outputRe, __global void *outputIm, uint outoffset, __global void *userdata, double fftoutputRe, double fftoutputIm) With LDS void <postcallback_func> ( __global void *outputRe, __global void *outputIm, uint outoffset, __global void *userdata, double fftoutputRe, double fftoutputIm, __local void *localmem) |
| C2R Single Precision | Without LDS void <postcallback_func> ( __global void *output, uint outoffset, __global void *userdata, float fftoutput) With LDS void <postcallback_func> ( __global void *output, uint outoffset, __global void *userdata, float fftoutput, __local void *localmem) |
| C2R Double Precision | Without LDS void <postcallback_func> ( __global void *output, uint outoffset, __global void *userdata, double fftoutput) With LDS void <postcallback_func> ( __global void *output, uint outoffset, __global void *userdata, double fftoutput, __local void *localmem) |
Parameters
output : The base pointer of the output buffer for C2R and Interleaved R2C/C2C transforms outputRe : The base pointer of the “Real” output buffer for Planar R2C/C2C transforms outputIm : The base pointer of the “Imaginary” part output buffer for Planar R2C/C2C transforms outoffset : Index of the current element of the output buffer from the start userdata : Buffer containing optional caller specified data. The userdata pointer is useful for passing any supplementary data to the callback function. For example, buffer having convolution filter data or any scalar value. The userdata can be of any custom data type/structure, in which case, you have to declare the custom data type and include it along with the callback function string. fftoutput : The result computed by clFFT for the element corresponding to outoffset argument localmem : Pointer to local memory. This memory is allocated by library based on the size you specify and is subject to local memory availability.